*크롬으로 보시는 걸 추천드립니다*
https://arxiv.org/pdf/2311.04635v1
종합 : ⭐⭐⭐⭐
1. 논문 중요도 : 4 점
2. 실용성 : 4 점
설명 : 추천 시스템에 주요 트렌드를 적용한 논문
- Cross Network를 활용하여 Feature Interaction을 활용
- Information Gate를 활용하여 중요한 상호작용(Interaction)을 동적(dynamic)으로 필터링
- Embedding Layer의 Field별 중요도에 따라서 dimension 압축
- 2023년 기준으로 SOTA (24년도에는 DCVN v3가 리더보드를 갱신했지만 그 차이는 크지 않음)
( * 개인적인 의견이며, 제 리뷰를 보시는 분들에 도움드리기 위한 참고 정도로 봐주세요)
딥러닝 분야에서 최근 트렌드는 3가지 입니다.
1. Gate를 활용한 MoE 전략으로, 25년 초 화제가 되었던 DeepSeek 핵심 전략 중 하나입니다.
2. 적극적인 임베딩 활용하여 서비스화 하고 있습니다.
3. Multi-Task Learning을 통한, 하나의 모델로 여러 문제를 해결합니다.
추가로, 추천 분야에서는 Cross Network를 사용하고 있습니다.
- Cross Network는 입력 Feature나 임베딩들의 상호작용(Interaction)을 딥러닝 구조에서 잘 활용하기 위한 전략입니다.
※ 추천 관련 상위 모델 리더보드 (https://paperswithcode.com/sota/click-through-rate-prediction-on-criteo)

주요 추천 AI모델의 트렌드를 파악하기 위한 중요 논문인 GDCN (Gated Deep Cross Network)를 리뷰하고자 합니다.
GDCN 논문 소개
- GDCN(Gated Deep Cross Network)의 의의
- 추천에서의 핵심은 Feature의 interaction을 효과적으로 모델링하는 것
- 기존의 추천 모델인 DCN에는 3가지 제한점(challenge)이 있었음
1. Feature interaction order가 증가할수록 성능이 저하되는 경향
2. 예측 결과에 대한 해석력(interpretations) 부족하며, 특히 high-order feature interactions에서 문제가 심화됨
3. Embedding Layer에서 중복되는 parameters가 매우 큼
- Gated Deep Cross Network (GDCN) 제안
1. Explicit(명시적인) high-order feature interactions을 활용하여 추천 성능을 높임
2. information gate를 활용하여, 중요한 상호작용을 동적(dynamic)하게 필터링
- Field-level Dimesion Optimization(FDO) 제안 → Field 별 중요도에 따라서 Embedding dimension 압축
: 23% 적은 파라미터 수로 성능을 유지함
- 더 적은 모델 파라미터로도 좋은 성능을 보여주며, 5개의 데이터셋에서 SOTA 성능을 달성
- 추천 결과에 대한 해석 가능성을 보여줌
추천 AI 분야의 배경
- Higher-order란?

○ 일반적인 High-order interaction 예시
- 1차 Interaction : x1, x2, x3
- 2차 Interaction : x1*x2, x1*x3, x2*x3
- 3차 Interaction : x1*x2*x3
○ DNN구조에서 Layer가 깊어질수록 더 깊고 복잡한 고차(High-order) interaction을 학습할 수 있는 잠재력을 가짐
- 추천 분야의 CTR 예측에서의 기본 요소
○ Feature Embedding
- 텍스트나 이미지에서 추출된 임베딩 입력
- category Feature의 embedding Layer 활용 등
○ Feature Interaction
- Feature 간의 상효 작용
- 예시 : 50대인 여성(50 Age x Female) 등
- 많은 최신 논문들이 Feature Interaction을 효과적으로 사용하기 위한 Architecture를 제안하고 있음
: 과거에는 Low or Fixed order를 사용했다면, 지금은 Dynimic High-order Feature Interaction을 하도록 발전 중
○ Prediction
- CTR 예측 스코어 (0 ~ 1)
- 기존 제안된 모델에서의 제한점
○ Order가 높아질수록 효과가 떨어짐
-Interaction layer가 깊어질수록 interaction degree가 높아짐 → interaction 수가 지수(exponeneial)로 급증하게 됨
-즉, Interaction layer가 깊어질 수록 더 많은 고차원 상호작용을 생성할 수 있음
-그러나, 모든 상호작용이 성능 향상에 도움이 되지 않음 → 오히려, 계산 복잡도는 증가되지만 성능은 하락하게 됨
: Sub-optimal에 빠져 성능 저하 발생
: interaction order가 3차가 넘어가면 성능이 저하됨을 확인
※ High-order interaction에서 긍정적인 영향력을 가진 것만 사용하도록, Feature Interaction의 noise를 줄여야 함
○ 추천 모델 결과의 해석력 부족
- DNN 모델은 implicit(함축적인) Feature interaction을 사용
- 모든 Feature interaction에 동일 가중치
- 최근 Sefl-attention 메커니즘을 시도는 있으나, 모든 Feature를 융합(Fuse)하는 경향이 있어 각각의 interaction의 중요도를 구별하기 어려움
: 위 사항들로 인하여, 모델의 해석력이 부족함
○ 임베딩 레이어에서 중복 파라미터가 존재
- 일반적으로, 어떤 임베딩의 Field는 작은 dimension이 필요함에도 모든 Field에 동일한 임베딩 차원을 가정
- 방대한 중복 파라미터가 생성됨
- 수동으로 Embedding dimension을 축소 시, 성능저하가 유발됨
- 대부분의 방법론에서는 Non-Embedding para. 를 줄이는 방향으로 개선.
: 예를 들어, DCN-v2에서는 \( d_f = (\text{feature number})^{0.25} \)으로 모든 Field를 공통적인 로직으로 줄임
: 각 필드별 중요도를 반영하진 못함
- DNN과 Cross Network의 차이
○ DNN은 함축적인(Implicit) Feature interaction을 학습
○ Cross Network는 명시적인(Explicit) Feature interaction을 학습
- Cross Network 기본 구조

○ Stacked Structure
- 1 단계 : Embedding Layer - 데이터의 카테고라나 속성을 나타내는 Field 별로 Embedding을 구성
- 2 단계 : Explicit interaction 포착 - Input과 Dense Layer output과 element-wise 곱함 (= Cross Network)
- 3 단계 : Implicit interaction 포착 - 일반적인 Dense Layer로 2 단계에서 나온 정보를 더 심층 및 복합적으로 모델링
○ Parallel Structure
- 1 단계 : Embedding Layer 동일
- 2 단계 : Explicit과 Implicit을 분리하여 병렬로 포착 - 두 개의 병렬 Network를 통해, 함축 및 명시적인 interaction을 공동(jointly)으로 포착
- 3 단계 : 두 개의 Network를 concat
○ 공통적인 단점
1. 더 고차원이 될 수록 성능이 하락
2. 해석력이 부족
- Gating Mechanism 이란
○ 게이팅 매커니즘은 GRU나 MMoE(Multi-Task Learning)에서 많이 사용
- gate를 통해 핵심 Feature를 선택하고 중요도에 따라서 information 흐름을 제어함
- Multi-Gate Mixture-of-Experts(MMoE) : 여러 개의 Gating Network를 통해 가중치를 부여하고 작업(Task) 목적 별 중요도 가중치를 부여
○ GDCN에서는 inforamtion Gate를 적용하여 각 Cross Layer에 Cross Feature의 중요도를 식별하도록 디자인
- 특히, GDCN에서 inforamtion Gate의 역할은 더 High-order Interaction을 잘 활용하고 이 때 발생되는 Noise를 완화시키고, 해석력을 제공
GDCN 모델 구조

- GDCN 소개
○ DCN-v2를 확장하여, Cross Layer 별로 Information Gate를 적용하여 적응적(adaptively)으로 Cross Feature를 필터링
- 기존 DCN-v2에서는 모든 피쳐에 동일(Uniform)한 기여도를 부여
- Deeper High-order cross information을 활용하고, 모델의 해석력도 추가됨
- https://github.com/anonctr/GDCN/blob/main/models/GDCN.py
GDCN/models/GDCN.py at main · anonctr/GDCN
The code of GDCN. Contribute to anonctr/GDCN development by creating an account on GitHub.
github.com
- Gated Cross Net(GCN) Layer 설명
○ 명시적(Explicit) Feature Cross를 Information Gate와 결합
\( \mathbf{c}_{l+1} = \mathbf{c}_0 \odot \underbrace{\left( \mathbf{W}_l^{(c)} \times \mathbf{c}_l + \mathbf{b}_l \right)}_{\textit{Feature Crossing}} \odot \underbrace{\sigma \left( \mathbf{W}_l^{(g)} \times \mathbf{c}_l \right)}_{\textit{Information Gate}} + \mathbf{c}_l \)

- \( \mathbf{c}_0 \) : Embedding Layer로 부터의 입력값 ( = 1st order features)
- \( \mathbf{W}_l^{(c)} \) : 학습 가능한 DxD 크기의 가중치 행렬 - c(cross), g(gated)
○ Feature Crossing 수식 설명
- 1st-order Feature \( \mathbf{c}_0 \)와 \( (l)\text{-th} \) order feature간의 교차
- bit-level( = 임베딩 벡터의 개별 요소 단위) 결합
○ Information Gate 수식 설명
- \( (l+2)\text{-th} \) order feature의 중요성 적응적으로 학습하도록 Soft Gate 역할
※ \( (l+2)\text{-th} \) 인 이유 : 1st-order의 Layer가 \( \mathbf{c}_0 \)
- Sigmoid 함수를 활용하여 Gate Value 출력 \( \sigma \left( \mathbf{W}_l^{(g)} \times \mathbf{c}_l\right) \)
○ Feature Cross와 Information Gate를 거치면, 1st-order 부터 \( (l+2)\text{-th} \)h order 까지 모든 Feature Interaction을 포괄하게 됨
- GDCN의 DCN-V2와의 연관성
○ GDCN은 DCN-v2의 일반화 버전 : Gate가 제거되거나 Gate Value가 전부 1이면 DCN-v2와 동일
- Bit-level 단위별로 동일한 중요도를 가졌는지 여부의 차이
- DCN-v2에서는 저차원 전문가(= subspace)와의 곱으로 활용.
: Non-embedding para.를 줄일 수 있었음. → 초기값으로 64 dim이나 10~25%로 줄이는 것을 추천
\( \mathbf{x}_{l+1} = \sum_{i=1}^{K} G_i(\mathbf{x}_l) E_i(\mathbf{x}_l) + \mathbf{x}_l \)
\( E_i(\mathbf{x}_l) = \mathbf{x}_0 \odot \left( U_l^i \left( V_l^{i\top} \mathbf{x}_l \right) + \mathbf{b}_l \right) \)
- Field-level Dimension Optimization (FDO)를 활용
○ embedding dimension은 정보를 인코딩하는 능력을 결정. 하지만 대부분 같은 차원을 적용
○ DCN-V2에서는 Feature 수^(0.25)를 적용
○ 사후적으로 Independent 와 intrinsic importance를 고려한 방법(FmFM에 영감을 받음)
- 1 단계 : 16차원으로 고정하여 모델을 훈련
- 2 단계 : PCA를 활용하여, 각 필드의 임베딩 테이블의 singular values를 계산
- 3 단계 : information utilization (i.e., information ratio)를 활용하여 최적의 차원을 결정
- 4 단계 : 3단계에서 결정된 최적에 필드 별 차원을 적용하여, 새모델로 다시 학습
○ information ratio 80~95%일 때, 대부분 차원은 2~15으로 줄어듬
- 필드 수보다는 필드의 중요도가 모델 성능과 관련이 있음 (sec 5.5에서 자세히 다룸)
- 80% information ratio 기준으로도 SOTA 모델을 능가함
- 37%으로 임베딩 차원을 줄일 수 있음
※ GDCN 모델의 Field 별 차원 수
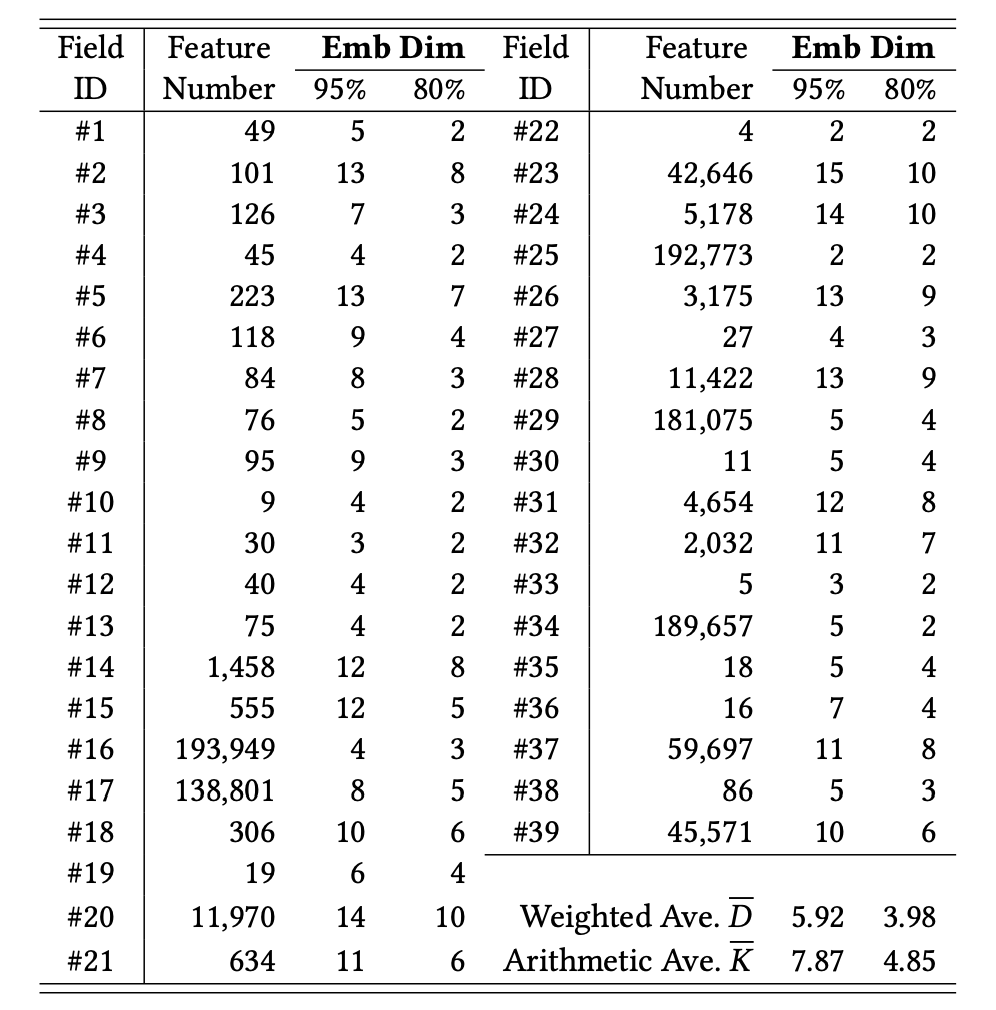
GDCN 실험 결과
- 실험 설정
○ 데이터 셋 : 학습 : 평가 : 테스트를 각각 8 : 1 : 1 비율로 나눔
- 필드내에서 빈도가 낮은 피쳐는 "<UNK>"로 처리
○ 평가 지표 : AUC와 LogLoss(CrossEntropy)
- 10회 반복 실험
- 추가 : T-Test 검증을 통해, 통계적 유의성 확인
: 추천 분야에서는 0.001-level의 상승도 크게 개선된 것으로 여기고 있음
○ 학습 방법 (default 설정)
- Adam(lr=0.001) optimizer로 통일
- Reduce-LR-Plateau Scheduler(patience 3, reduce 1/10) 사용
- Early Stopping(patience 5) 사용
- Batch Size : 4096
- Embedding dimension : 16
- DNN component : 400-400-400(drop-out 0.5)으로 통일
- GCN component : 3 layer 사용
- ReLU activation 사용
- 실험 결과 - 추천 성능
○ Stacked 계열의 실험 결과
- High-order기반 model이 first- 나 second-order 기반 모델보다 좋은 성능
- Explicit(명시적인) 및 implicit(함축적인) 모두를 활용한 High-order 계열의 모델이 대체로 우수
- 제안한 GDCN-S 모델(AUC 0.8158)이 다른 모든 Stacked Baseline을 뛰어넘음
: AUC 평균 0.28%, LL 평균 2.7% 더 우수

○ Parallel 계열의 실험 결과
- Explicit(명시적인) 및 implicit(함축적인)을 통합하는 것이 효과적임
- GDCN-P가 전체 Stacked나 Parallel 모델 중 가장 우수한 성능
: AUC 평균 0.46%, LL 평균 5.57% 더 우수

- 실험 결과 - Deeper High-order Feature Crossing
○ Cross Network를 깊게 쌓았을 경우 성능 추이 확인
- Cross Network가 깊어짐에 따라서 성능이 증가하나, 4개 이상 부터는 저하되는 특징을 보임
: Higher-order Cross feature가 불필요한 노이즈가 되어버림(Overfitting & Degradation)
- 제안한 GCN에서는 유용한 Cross Feature를 식별 및 선별하는 것을 확인
: 유일하게 GCN에서만 Layer 4 이상으로 늘어나도 성능개선이 지속됨

○ Cross Network Depth에 대한 고찰(GDCN-P)
- 설정 : Cross Depth를 16까지 증가 실험. DNN Depth는 Overfitting 방지를 위해 3으로 고정
- DNN의 필요성 재확인
1) DNN이 없는 GCN 모델에서 Cross Network가 계속 높여도 DNN이 있는 GDCN의 성능이 더 우수
2) DNN이 있으면 더 빠르게 학습이 수렴하도록 도와줌. Cross Layer 4~6 depth로도 성능이 수렴됨
- Layer가 깊어짐에 High-order Cross feature의 유용성 폭은 점차 감소됨
1) 필요한 Cross Feature order는 무한하지 않음
2) 즉, 8~10차수만 되어도 유용한 Cross Feature는 확보가 됨

- 실험 결과 - 추론 결과의 해석력 확보
○ 추론 해석력 : AI 추천 모델의 예측 결과를 이해하고 신뢰도를 높임
- 모델 및 Instance(= 개별 유저) 관점에서의 "static" 및 "dynamic" 해석력을 제공
○ 모델 관점에서의 "static"한 해석력을 제공
- "static" 해석력이란 : Cross Weight Matrix를 통해 얻을 수 있는 모델을 이해할 수 있는 정보
- 본 논문에서는 GCN의 Cross Weight Matrix \( (\mathbf{W}^{c}_l) \)를 통해, 서로 다른 Field간의 상호작용의 중요도를 확인
: Frobenius norm을 사용하여, \( (\mathbf{W}^{c}_F) \)의 값 크기가 클 수록 상호작용의 중요도가 높음
※ Frobenius norm : \( \|A\|_F = \sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n} |a_{ij}|^2} \)
- Bit-wise나 Block-wise 단위로 해석력을 제공 가능
: Field 별 weight matrix의 Frobenius norm 을 계산하면 Block-wise, weight 개별 값은 bit-wise 단위의 상호작용 중요도

- 그림 예시는 Field의 Block-wise 기준으로 중요도를 시각화 한 결과로서, 1st-order와 input간의 상호작용 중요도를 확인 할 수 있음
○ Instance(= 개별 유저) 관점에서의 "dynamic"한 해석력을 제공
- "dynamic" 해석력이란 : 인스턴스(예시 : 유저)단위의 추론 결과를 이해하는 해석력을 제공
- 두 개의 인스턴스를 선택하여, Gate Weight( \( \sigma \left( \mathbf{\boldsymbol{W}}_l^{(g)} \times \mathbf{\boldsymbol{c}}_l \right) \) )를 시각화
- bit-wise 단위의 dynamic 해석 가능성 : 인스턴스의 Field 별 Gate Weight를 시각화
- Field-wise 단위의 dynamic 해석 가능성 : Field 별 Gate Weight 값을 평균
- Information Gate는 sigmoid를 사용하기에 0.5가 기준이 되어 보다 클 수록 영향이 높음

- 시각화 결과 Lower-order cross feature가 더 중요함을 확인
: 1st layer에서 Gate Information이 0.5 이상인 경우가 3rd layer보다 많음
: 고차 Cross Feature를 Gate를 활용하여 적응적(Adaptively) 필터링해야하는 이유를 재확인할 수 있음
○ 해당 해석력 및 시각화 결과를 바탕으로 사후적으로 Cross Feature의 이름을 짓고, 직접 해당 Cross Feature를 만들 수 있음
- 실험 결과 - FDO(Field-level Dimension Optimization) 효율성
○ FDO 80% 적용까지, Parameter는 77% 절감하면서 성능을 유지할 수 있음.
- FDO 98%로만 줄여도 55.2% 절감. 그럼에도 성능은 향상
○ 중요도에 따라서 Field별로 적응적으로 dimension을 축소하여 모델의 크기는 크게 줄이면서 성능을 유지할 수 있었음
- 중요도가 높은 Field에는 상대적으로 차원이 커지도록 반여함
○ FDO 적용 시, 학습시간 절감효과는 없었음

Conclusion
○ GDCN은 명시적인(Explicit) Feuture와 DNN 함축적인(implicit) 교차 Feature를 하여 추천 성능을 높임
○ GDCN은 Information Gate를 사용하여, cross feature의 중요도를 판별하여 선별
○ model과 instance 레벨 모두에서 해석력을 가져, 모델 추론 결과를 이해하는데 도움을 줌
○ FDO를 사용하여, 중요도에 따른 field별 embedding layer의 차원을 축소함
- 모델 크기는 77% 축소하면서, 성능은 유지함
○ GDCN-P 및 FDO를 통해 SOTA 달성
마치며
○ 2023년에 나온 논문으로서 추천 분야의 주요 트렌드를 담고 있습니다
1. Gate를 활용한 중요도 판별
2. Cross Network를 활용한 Interaction Feature의 활용을 극대화
○ 추천 분야에서는 추론 속도도 중요하기에 모델의 사이즈를 줄이는 것이 중요한데, 그 해결책을 제안 및 증명했습니다.
○ 구현이 간단하여 실용성이 매우 높습니다.
다음 논문으로는 Multi-Task 분야이기도 한 MoE(Mixture-of-Experts)를 다루려고 합니다.
LLM 분야(예 : deepseek 등)에서 핵심적으로 사용하고 있는 기술이지만, 추천 분야에서도 매우 중요한 기술이기 때문입니다.
'발전중인 AI > 추천(Recommendation)' 카테고리의 다른 글
| Mixture-of-Experts 추천 시스템 개요 - ② (0) | 2025.04.06 |
|---|---|
| Mixture-of-Experts 추천 시스템 개요 - ① (1) | 2025.03.14 |
| [논문요약] DNN for YouTube(2016) - 추천 딥러닝 모델의 바이블 (0) | 2022.02.15 |
| [논문요약] 딥러닝 관련 추천 모델 - Survey(2019) (0) | 2022.02.15 |
| 추천 시스템 기본 - 협업 필터링(Collaborative Filtering) - ② (0) | 2021.08.10 |