*크롬으로 보시는 걸 추천드립니다*
대표적 추천 시스템인 협업 필터링(Collaborative Filtering) 중 Memory-Based Approach에 대해서 다루어보았습니다
https://kmhana.tistory.com/31?category=882777
Have A Nice AI
kmhana.tistory.com
지금 Part2 에서는
• 협업 필터링(Collaborative Filtiering)의 대표 접근법 Model-Based을 알아볼 예정입니다
- Matrix Factorization(행렬 분해)
- Neural Network(신경망)의 간단한 소개
• 협업 필터링(Collaborative Filtiering)의 한계
• 그 밖의 방법론 소개
(* 언제든지 부족한 부분 알려주시면 반영하겠습니다 ㅎㅎ 함께 공부해 나아가봐요)
협업 필터링 - Model Based Approach 이란?
○ 협업 필터링 - Memory Based Approach의 단점
1. 데이터가 축적 X or Sparse 한 경우 성능이 낮음
2. 확장 가능성이 낮음 ( ∵ 데이터가 너무 많아지면, 속도가 저하됨)
○ 극복 방안 - Model based Approach
• 기계학습(Machine Learning) 알고리즘을 통해, 사용자(User)가 아직 평가하지 않은 아이템(Item)의 평점을 예측
• 기본 아이디어 : 사용자의 선호도는 소수의 Hidden Factor로 결정될 수 있다!
- Hidden Factor를 Embedding 이라고도 부름
* Embedding 이란 : Item과 User에 대한 압축된 저차원(Low-dimensional) Hidden Factor
• 행렬 분해(Matrix Factorization : MF ) 등을 사용
- 비모수적(Non-Parametric) 방법
- 행렬 분해(Matrix Factorization : MF ) 알고리즘
- 딥러닝(Deep Learning) 기반 방법

• 행렬 분해(Matrix Factorization : MF )는 Loss Function과 제약(Constraints) 조건이 있는 최적화 문제로 공식화됨
- 예를 들어 : Non-Negative Matirx(NMF) 분해 방법은 음수가 아닌 요소(Element)가 결과로 나와야 함
○ 행렬 분해(Matrix Factorization : MF ) 란

• 예시 : User 및 Item 모두에 대해 5차원 임베딩( n_factor = 5 ) 가 있다고 가정
- User-Item 행렬을 "User-X",와 "Item-A" 행렬로 변환
• 행렬 분해(Matrix Factorization)는 여러 방법을 수행 가능
- Orthogonal Factorization(Singular Vector Decomposition(SVD) 특이값 분해 )
- Non-Negative Matrix Factorization(NMF)
- Probabilistic Factorization(PMF) 등
※ Sigular Vector Decomposition(SVD ; 특이값 분해) 란?
※ Sigular Vector Decomposition(SVD ; 특이값 분해) 란?
* 고려대 강필성 교수님 자료와
https://angeloyeo.github.io/2019/08/01/SVD.html와 https://darkpgmr.tistory.com/106 를 함께 참고했습니다
• 특이값 분해는 직교(Orthogonal)하는 벡터 집합에 대한 선형 변환
$$ A = U \Sigma V^{T} $$
- \( A : m \times n \) Rectangluar Matrix
- \( U : m \times m \) Orthogonal Matrix
- \( \Sigma : m \times n \) Diagonal Matrix
- \( V : n \times n \) Orthogonal Matrix
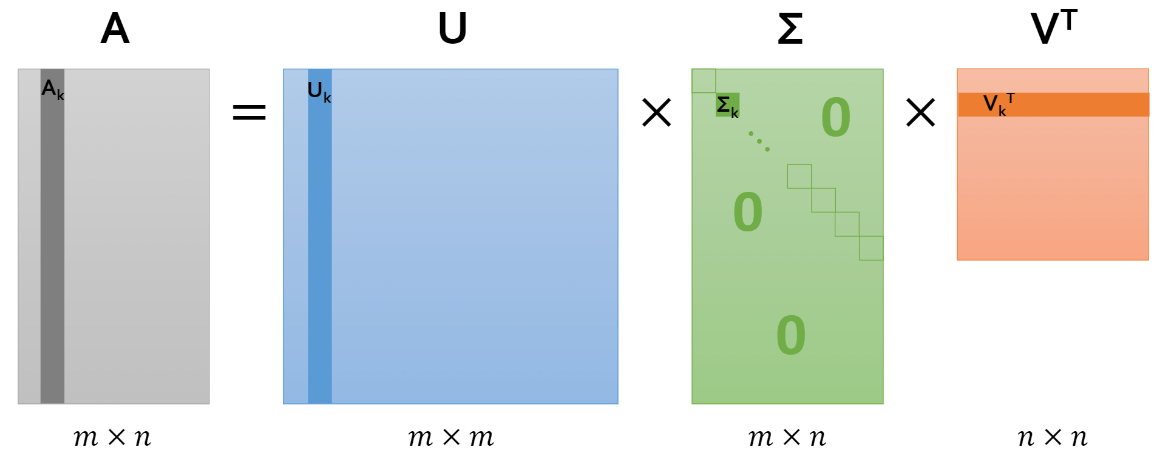
• 수식을 풀면
$$
\begin{matrix}
A = U \Sigma V^{T}
\\
= \sigma_{1}\vec{u_{1}}\vec{v_{1}}^{T} + \sigma_{2}\vec{u_{2}}\vec{v_{2}}^{T} + ... + \sigma_{m}\vec{u_{m}}\vec{v_{m}}^{T}
\end{matrix}
$$
$$
\begin{matrix}
A = U\Sigma V^{T}
\\
AVV^{T} = U\Sigma V^{T}
\\
AV = U\Sigma
\end{matrix}
$$
- \( A\vec{x} \)와 \( A\vec{y} \)를 만족하는 경우는 한 번만 있지 않음
- \( A \)라는 벡터를 선형 변활 할 때, 조금씩 길이가 변함
- 이 값들을 Singular Value라고 하며, \( \sigma_{1},\sigma_{2} ... \) 를 의미함
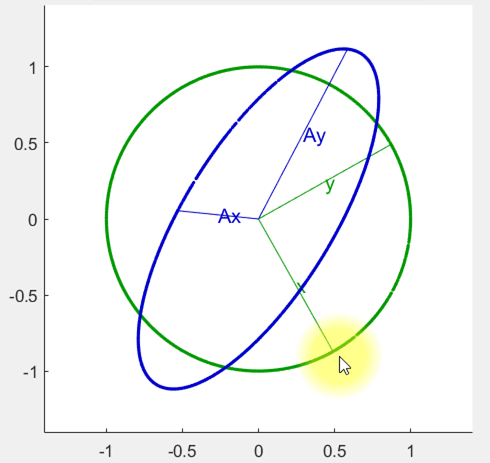

- \( AA^{T} \) 고유값(Eigen Value)과 고유 벡터(Eigen Vector)를 통해 분해할 수 있음
• 활용방안 :

- 분해된 행렬의 \( \Sigma : m \times n \)를 축소시킴

• 각각의 User-X Embedding과 Movie-A Embedding은 여러 요약적인 특성을 나타낼 수 있음
- Latent Sementic Analysis라고도 함
* Latent : 잠재적인
* Latent : 의미론적인
- Movie-A Embedding 예시 : 1) 공상과학과 관련된 요소 2) 최근 영화인지에 대한 요소 등
- User-X Embedding 예시 : 1) 공상과학영화를 얼마나 좋아하는지 2) 최근 영화를 얼마나 선호하는지 등
- 실제로는 각 Factor가 무엇을 의미하는지 정확히 알 수 없음
• User-X Embedding과 Movie-A Embedding의 내적 값이 높을수록 User-X에게 Movie-A가 더 좋은 추천을 의미
○ 비모수(Non-Parametric)적 접근법
• Memory-based 추천 시스템의 아이디어와 유사
- Memory-based는 사용자(User)와 아이템(Item)의 유사도를 사용
- 가중치 평균을 사용해서, 사용자의 아이템(Item)의 평가(Rating)를 예측함
• 차이점 : Pearson Correlation이나 Cosine Similarity를 사용하는 대신, Unsupervised Learning 모델을 사용
- KNN와 같은 Unsupervised Learning 모델을 사용
- K개의 이웃(Neighbor)한 사용자 수로 제한하여, 시스템의 확장성을 높임
○ 딥러닝(Deep Learning)적 접근법

• 행렬 분해나 Similarity 행렬을 사용한 자료는 많으나, Deep Learning을 활용한 협업 필터링 관련 자료는 부족
• 행렬 분해의 확장으로 생각할 수 있음 → 행렬 분해 결과를 Input으로 사용 가능
- SVD나 PCA는 희소(Sparse) 행렬을 2개의 낮은 Rank의 직교 행렬(User-X, Item-A)로 분해
- Deep Learning은 이 Embeddding을 직교할 필요 없이, 자체작으로 학습하길 원함
- User-Item의 조합으로부터 Look-up(조회)가 됨
- 비선형(Non-linear : ReLU)나 선형(Linear), Sigmoid Layer 사용
- 최적화 알고리즘(SGD, Adam)을 사용하여 가중치를 학습
협업 필터링의 한계
https://brunch.co.kr/@biginsight/15
04화 추천 알고리즘, 내 취향을 어떻게 그렇게 잘 알아?
집단지성에서 파생된 협업 필터링과 최신 추천 알고리즘 알아보기 | 평범한 다수가 똑똑한 소수보다 낫다. 여러분은 이 말에 동의하시나요? 제임스 서로위키(James Surowiecki)는 『Wisdom of Crowds』라
brunch.co.kr
○ 협업 필터링 한계
1. 콜드 스타트(Cold Start)
- "새로 시작할 때의 곤란함"
- 데이터가 중요(User-Item 행렬이 충분하게 구축되어야 함)
- User-Based 방법 : 신규 사용자의 행동이 기록되지 않으면, 어떤 아이템(Item)도 추천 X
- Item-Based 방법 : 신규 상품이 출시가 되더라도 추천 X
→ 시스템이 아직 충분한 정보를 모으지 않으면, 추천 불가
2. 계산 효율성 저하
- 협업 필터링(Collaborative Fitlering)은 계산량이 많은 알고리즘
- 사용자가 많아질수록 계산 시간 증가
- 사용자가 많아야 정확한 추천 결과를 내지만, 동시에 계산 시간도 증가됨
3. 롱테일(Long-Tail) 문제

- "파레토 법칙" : 전체 결과의 80%가 전체 원인의 20 % 에서 발생되는 현상
- 사용자들이 관심을 많이 보이는 소수의 인기 있는 콘텐츠를 주로 추천하게 됨
- 품질 좋은 Long-Tail 아이템은 추천되지 못하여, 추천의 다양성이 떨어지게 됨
협업 필터링의 한계 극복 방안
○ 협업 필터링 한계 극복을 위한 방안
1. 콘텐츠 기반 필터링(Contents-Based Filtering)
• 콘텐츠에 대한 분석을 기반으로 추천
- 예시 : 영화 - 감독, 장르, 등장인물 등 / 상품 - 상품설명, 종류
• 장점 :
- 많은 사용자의 행동 정보가 필요하지 X
- 콜드 스타트(Cold Start) 문제 해소 가능
• 단점 :
1) 메타 정보의 한정성 : 상품의 프로파일을 모두 함축하는데 한계가 있음 → 정밀성이 떨어짐
2) 개인의 성향을 세부적으로 파악하기 어려움
• 방법 :
1) 50명의 태거(Tagger)에 의해서 사람이 직접 콘텐츠의 태그를 담
- 넷플릭스는 사람이 태그를 달아 콘텐츠를 5만 종으로 나눔
2) 기계학습 : 텍스트 마이닝으로 분석
2. 하이브리드(Hybrid) 추천 시스템
• "협업 필터링"과 "콘텐츠 기반 필터링"을 조합
1) 데이터 쌓이기 전 : 콘텐츠 기반 필터링을 통해, 콜드 스타트 문제 해결
2) 데이터 쌓이기 후 : 협업 필터링으로 추천의 정확성을 높임
3. 머신러닝 추천 시스템
• 사용자의 조회, 클릭 등의 사소한 행동까지 학습
• 사용자에게 추천할 후보군 제안 → 사용자의 반응을 학습 → 점점 더 정교한 결과 도출
마치며
○ Part2에서 다룬 추천 시스템
• 협업 필터링(Collaborative Filtiering)의 대표 접근법 Model-Based을 알아볼 예정입니다
- Matrix Factorization(행렬 분해)
- Neural Network(신경망)
• 협업 필터링(Collaborative Filtiering)의 한계
• 그 밖의 방법론 소개
추천 시스템에서는 추천 결과의
①정확성
②다양성
③처리 속도
가 중요하다는 것을 알 수 있었습니다
다음 Part에서는 위에 세 가지 추천 요소를 높이기 위한 연구와 논문은 무엇이 있었는지 다루어볼 예정입니다!
'발전중인 AI > 추천(Recommendation)' 카테고리의 다른 글
| [논문요약] DNN for YouTube(2016) - 추천 딥러닝 모델의 바이블 (0) | 2022.02.15 |
|---|---|
| [논문요약] 딥러닝 관련 추천 모델 - Survey(2019) (0) | 2022.02.15 |
| 추천 시스템 기본 - 협업 필터링(Collaborative Filtering) - ① (0) | 2021.08.08 |
| 추천 시스템(Recommendation System) 시작 (0) | 2021.08.07 |