Activ Learning의 기본을 먼저 보고싶으신 분은, 이전 포스트
Active Learning 이란 - 기본
dsgissin.github.io/DiscriminativeActiveLearning/about/ About An introduction to the active learning framework, from classical algorithms to state of the art methods for neural networks. A new method..
kmhana.tistory.com
를 참고해주세요!
Active Learning의 기본적으로 알아야할
기초적인 쿼리전략(Query Strategies)를 간단하게 기술하고자 한다.
※ 쿼리전략(Query Strategies) 란? : 모델이 중요한 데이터를 찾기위한 전략
주요 기초 쿼리전략은 다음과 같다.
- Uncertainty Sampling
- Query By Committee
- Expected Model Change
- Density Weight Method
dsgissin.github.io/DiscriminativeActiveLearning/2018/07/05/AL-Intro.html
Introduction to Active Learning
The Basic Setup The idea of AL is, instead of just giving the learner a lot of data to learn from, to allow the learner to ask questions about the given data. In particular, the learner gets to ask an oracle (some human annotator) about the label of certai
dsgissin.github.io
사이트가 매우 좋아, 참고하였다.
1) Uncertainty Sampling
목표 : Decision Boundary에 가까운 샘플을 고르자.
설명 :
- '모델이 헷갈리는 데이터 = 학습에 필요한 데이터' 라는 생각에서 시작된다.
- 모델 입장에서 '헷갈리는 데이터'가 무엇일까? 라는 질문에 답은 Decision Boundary에 가까운 샘플이다.
- Decision Boundary에 가까운 데이터는, 즉, 헷갈리는 불확실성(Uncertainty)이 높은 데이터이다.
* Decision Boundary(결정 경계) : 카테고리의 분류(그룹)를 나누는 경계선
이 간단한 아이디어지만, 굉장한 일리가 있다.

방법 : 모델 입장에서의, 데이터의 불확실성(Uncertainty)를 측정하는 방식은 크게 3가지가 있다.

1. Top(Least) Confidence : 최대 확률값이 가장 낮은 데이터를 선별

- D-1 : top confidence는 0.9
- D-2 : top confidence는 0.5
- D-2의 top confidence < D-1 top confidence 이므로, top confidence가 낮은 D-2 선택
2. Margin Sampling : Top-1 confidence와 Top-2의 confidence의 차이가 낮은
- D-1의 마진 : 0.9-0.05 = 0.85
- D-2의 마진 : 0.5-0.3 = 0.2
- D-2 마진 0.2 < D-1 마진 0.85 이므로, Margin이 낮은 D-2 선택
3. Maximum Entropy : Entropy가 높은 데이터를 선택

- D-1의 Entropy : 0.171
- D-2의 마진 : 0.447
- D-2 Entropy 0.171 > D-1 Entropy 0.447 이므로, Entropy가 높은 D-2 선택
장점 :
1. 구현하기 매우 쉽다.
2. 성능이 생각보다 좋다.
3. 게다가, 딥러닝과의 연계도 생각보다 좋다.
4. 실험상, Uncertainty 기법 중, Maximum Entropy가 더 좋은 경우가 많았다.
※ 딥러닝에 Active Learning을 적용해보고 싶다면, Uncertainty(Entropy)를 강추한다.
'이렇게 간단한데 좋을까?'라는 의문이 들 수 있지만, 놀랍게 성과가 좋다.
단점 :
- Outlier에 영향을 많이 받음.
º Outlier인 데이터의 추론 확률 값은 모델이 예측하기 어렵다.
예를 들어, 3class 추론 확률값이 0.3, 0.3, 0.3으로 나올 가능성이 높으며, 이상치는 Entropy(Uncertainty)가 높다.
- 다른 치명적인 단점이 있다. 데이터를 선별할 때 Diversity(다양성)가 무시되었다.
º Diversity(다양성)가 무시 = 데이터 분포가 고려되지 X
이는 나중에 Core-set에서 Diversity(다양성)의 개념과 함께 설명하겠다.
2) Query By Committee
목표 : 여러모델을 통해, 마치 앙상블 처럼. 데이터를 선별해 보자
설명 :
- 여러 모델(Committee 위원회) 에서 투표하여 중요 데이터를 선별
- 여러모델에서 추론한 결과가 다르다 = 헷갈리는 데이터 = 불확실성(Uncertainty) 높음
- 앙상블의 Vote 개념을 Active Learning에서 사용
- Vote Entropy를 사용 할 수도 있다 ( Vote 확률 → Entropy 계산)

* M : 사용 모델 수(size of ensemble)
장점 :
- 구현이 어렵지 않다.
- 앙상블이 좋은건 당연하고, 이를 쓴 Active Learning의 효과도 좋다... 하지만!
단점 :
- 하나의 모델을 학습하는데 많은 비용이 드는 딥러닝에선 쓸수가 없다.
- 딥러닝 모델 학습 * 앙상블모델 수 * Active Learning 반복수 = Active Learning을 통한 자원절감 ↓↓↓
- 딥러닝을 쓰기엔, 배보다 배꼽이 큼
3) Expected Model Change
※ 이 방법에 대해서는 앞으로 중요하게 다루지 않을 예정이라. 장단점과 더불어 좀 더 설명드리고자 합니다.
목표 : 모델을 가장 잘 업데이트 할 수 있는 데이터가 중요하다!
설명 :
- 기대 Gradient가 가장 큰 데이터를 선별
- Expected Gradient Length(EGL) - arxiv.org/pdf/1612.03226.pdf
- RNN에서 class별 Norm Gradient를 계산(Backpropagation)한다.
- 계산된 기대값이 큰 데이터를 선별한다.
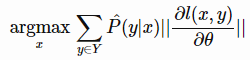
장점 :
- EGL 방식이 모델(Estimator)의 분산을 줄인다고 증명함
단점 :
- RNN(Speech)에 한정적인 성능을 보일 수 있음( 논문 저자는 몇까지 처리를 추가했음)
- CNN 실험에서는 낮은 성능을 보여줌 → Task마다의 성능이 크다는 건 큰 단점이다.

* 위의 그림은 실제 entropy의 순위와, AL(Active Learning)이 중요하게 판단하는 데이터 순위간의 연관성을 볼 수 있다.
- EGL은 Entropy(Uncertainty)와 전혀 상관이 없다.
- (b) 그림에서의 '빨간 원'은 EGL이 중요하게 판단한 데이터 이다.
: 침묵, 짧은 Speech, filler words(ex, Um..) 같은 데이터를 뽑았다고 한다.
→ 저자는 이 데이터가 모델학습에 중요한 데이터인지, Outlier 인지는 추가 연구가 필요하다고 남겨두었다.
º 위의 사실이 단점이라고 할 수는 없으나, 다른 실험들에서의 EGL의 성능이 낮게 나왔으며,
Uncertainty와 Gradient의 크기 간의 무상관을 원인으로 꼽고 있다.
º '이런 아이디어가 있었구나.' 정도 알아두면 좋을 것 같다.
Gradient의 크기를 활용하는 idea가 매우 좋다고 생각하지만 성능이 아쉽다.(더 좋은 AL로 개선하길 기원한다.)
4) Density Weight Method
※ 이 방법에 대해서는 앞으로 중요하게 다루지 않을 예정이라. 장단점과 더불어 좀 더 설명드리고자 합니다.
목표 : 이왕이면, 불확실성 + 밀집도가 높은 곳에 있는 데이터를 뽑자
설명 :
- Outlier에 취약한 Uncertainty의 단점을 커버하기 위해서, Density개념을 추가했다
- 밀집도가 높은 곳에 위치한 데이터는 Outlier일 가능성이 낮다.(Outlier는 Feature Space상, 멀리 떨어져 있다)
- 밀집도를 계산하는 방법에 따라서, 여러가지가 파생되었다.
대표 논문 :
Paper : Active Learning with Sampling by Uncertainty and Density for Word Sense Disambiguation and Text Classification - 2008
* 재밌는 아이디어가 있어서, 나중 이 논문에 대해서 한번 더 다룰 예정이다.
Paper : Active Learning With Sampling by Uncertainty and Density for Data Annotations - 2010

* 위의 그림에서, Decision Boundary와 가까운 A와 B data 중, 밀집도(Density)가 높은 B가 A에 비해서 우선된다.
- 밀집도를 계산하는 방법 : Sampling by Uncertainty and Density(SUD) - K-Nearest-Neighbor-based Density
º K = 20으로 설정 일때, S(x) = { s1, .. , Sk }
º data point x와 가까운 Nearest-Neighbor 20 개를 찾고 → cosine similarity를 계산하여, 더한다. = Density
º Density( k-Nearest-Neighbor의 Cosine similarity 합) X Entropy(Uncertainty)
º 가장 높은 Sampling by Uncertainty and Density (SUD)를 선택한다.

장점 :
- Outlier에 취약한 Uncertainty의 단점을 커버하기 위해서, Density 개념을 추가했다.
단점 :
- Outlier를 확실하게 방지 할 수 있지만, '밀집도(Density)가 높은 데이터가 꼭 좋은 데이터 일까?' 라는 의문이 있다.
- Unlabeled 데이터에서는 부적합할 수 있다.
5) 마치며
- 기본적인 쿼리 전략(Uncertainty, Committee, Gradient, Density)에 대해서, 다루었다.
- Uncertainty는 간단하지만, 꽤 좋은 성능을 보여준다.
- Active learning의 진입장벽이 낮아서, 실산업에서 많이 시도해볼만하다.
- 다음에는 좀 더 딥러닝에 적합한 Active Learning을 소개하고자 한다.
'실용적인 AI > Active Learning' 카테고리의 다른 글
| Active Learning을 위한 딥러닝 - Discriminative Active Learning (5) | 2021.02.02 |
|---|---|
| Active Learning을 위한 딥러닝 - Learning Loss for Active Learning (0) | 2021.02.02 |
| Active Learning을 위한 딥러닝 - Core-set (2) | 2021.02.02 |
| Active Learning 이란 - 기본 (2) | 2021.01.22 |
| 실용적인 Deep Learning 적용을 위한 시작 (1) | 2021.01.22 |